Training workshop on structural equation modelling (SEM) in R
Session 2: Confirmatory Factor Analysis & Covariance based SEM
Topic overview
1: CFA-SEM overview
2: CFA-SEM with Lavaan
3: Defining constructs
4: Developing the overall measurement model
5: Assessing measurement model validity
6: Specifying the structural model
7: Assessing structural model validity
CFA-SEM overview
What is SEM?
Not a one statistical “technique”
Integrates a number of different multivariate technique
Factor analysis
Regression
Simultaneous equation
Distinction between:
measurement model
structural model
What is SEM?
Measurement model
measurement part of a a full SEM model
confirmatory factor analysis
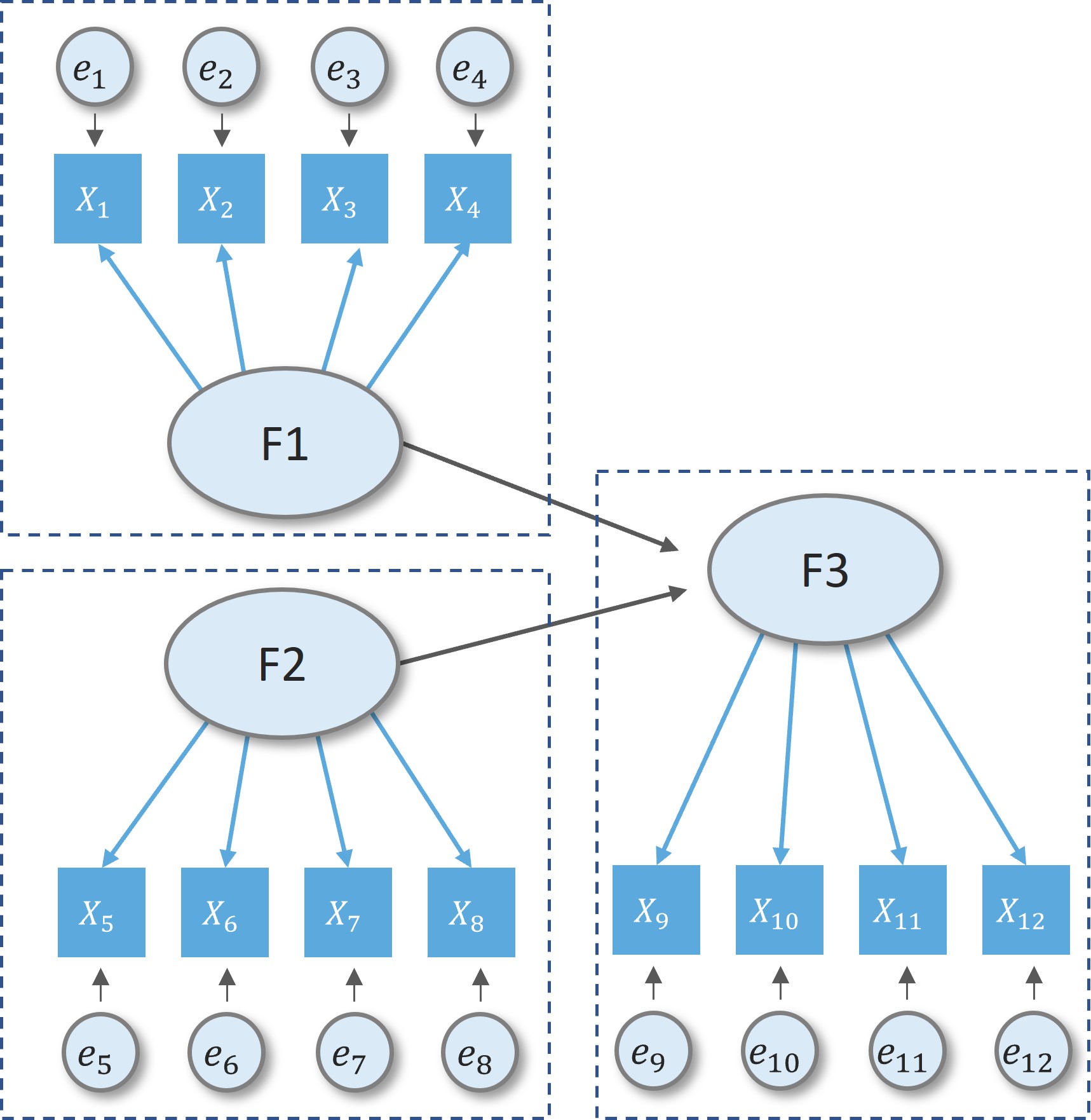
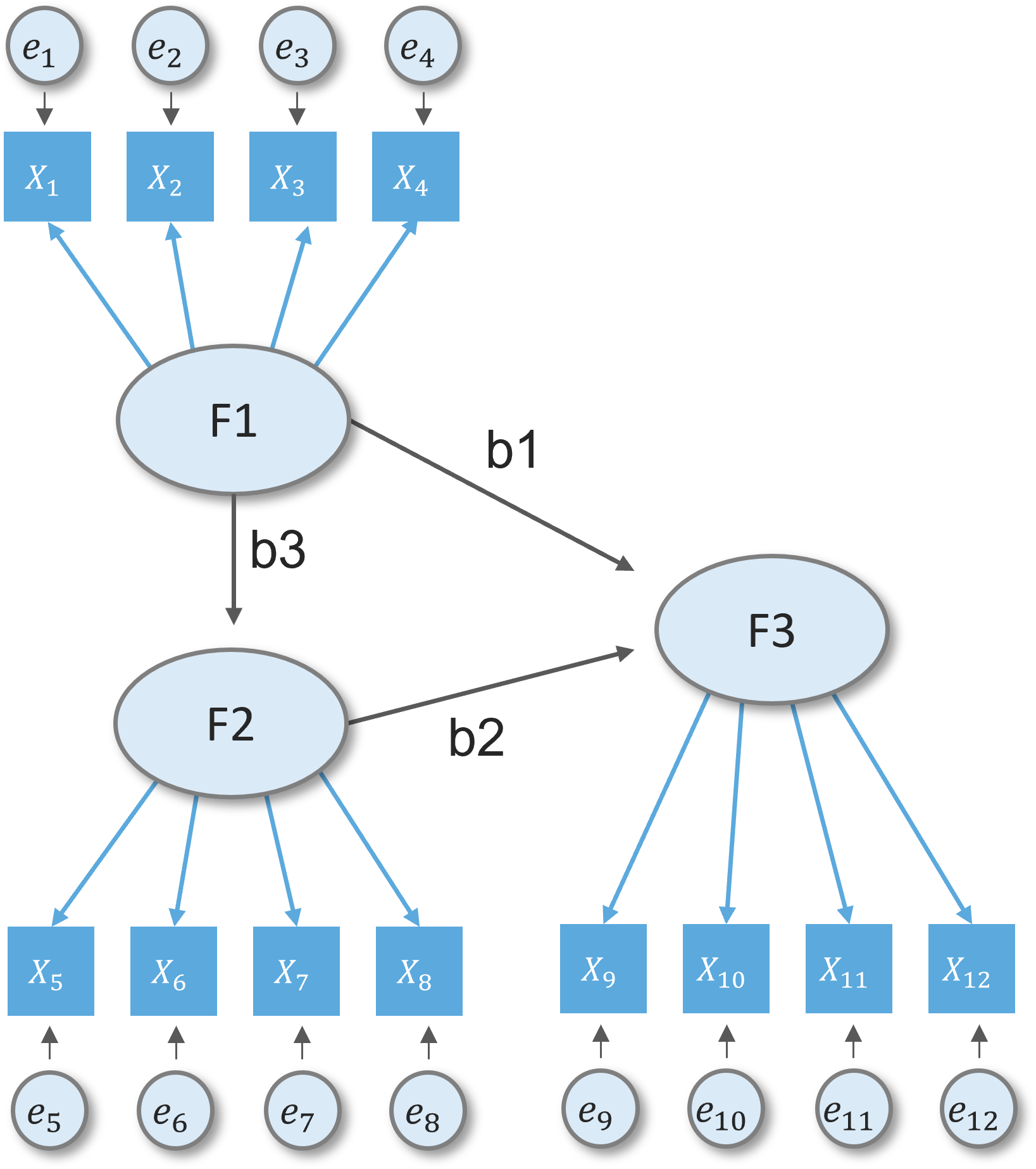
What is SEM?
Measurement model
measurement part of a a full SEM model
confirmatory factor analysis
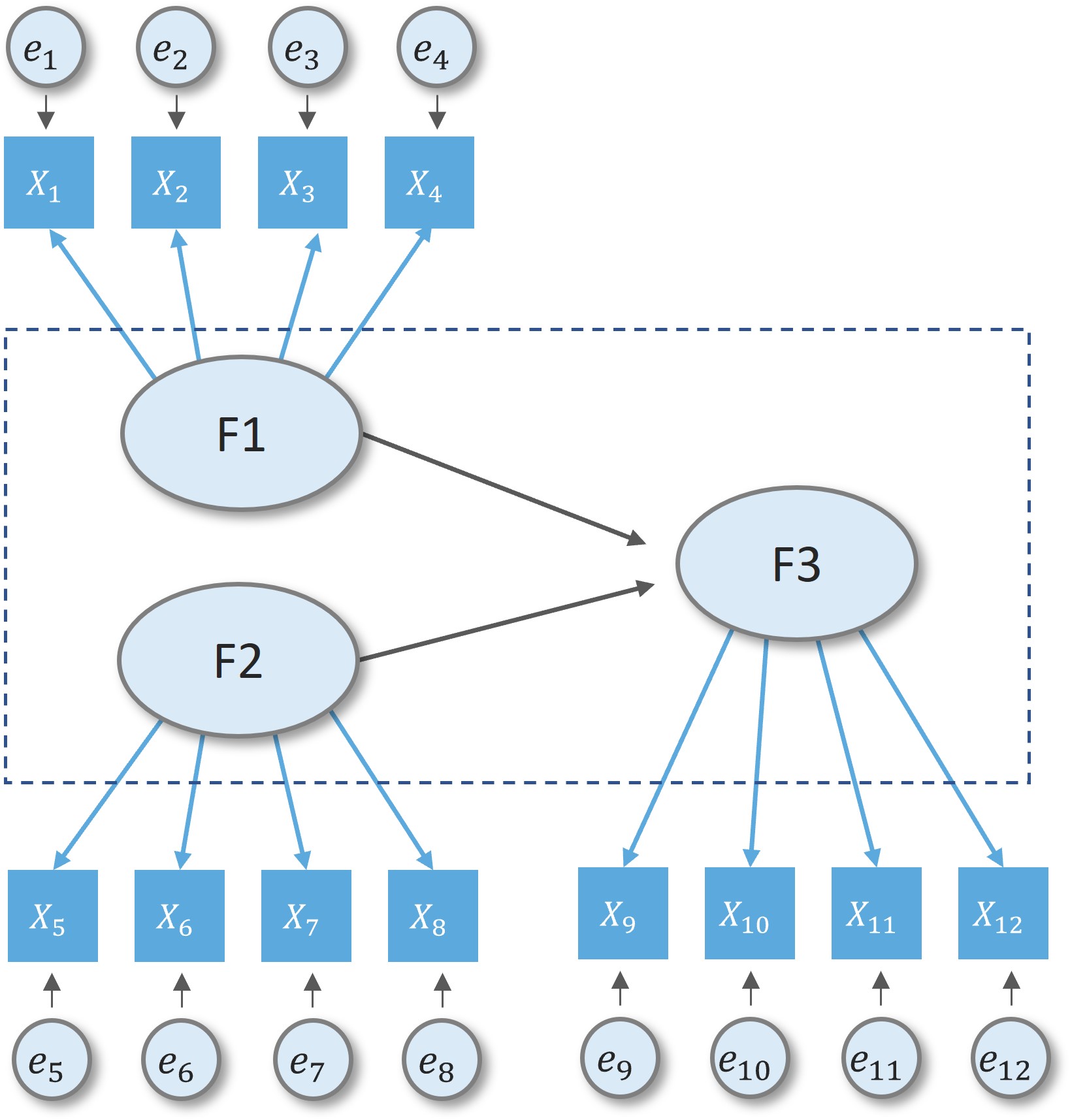
Structural model
relationship between constructs
full sem model is combination of measurement and structural component
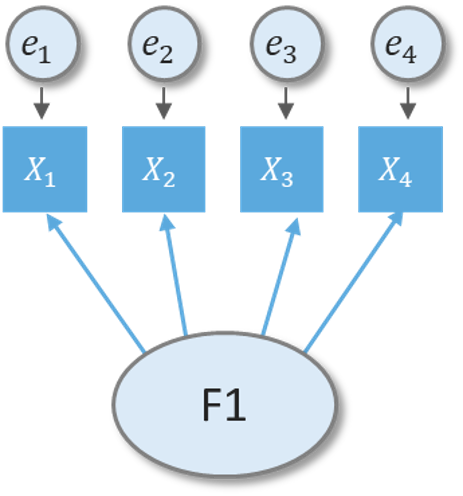
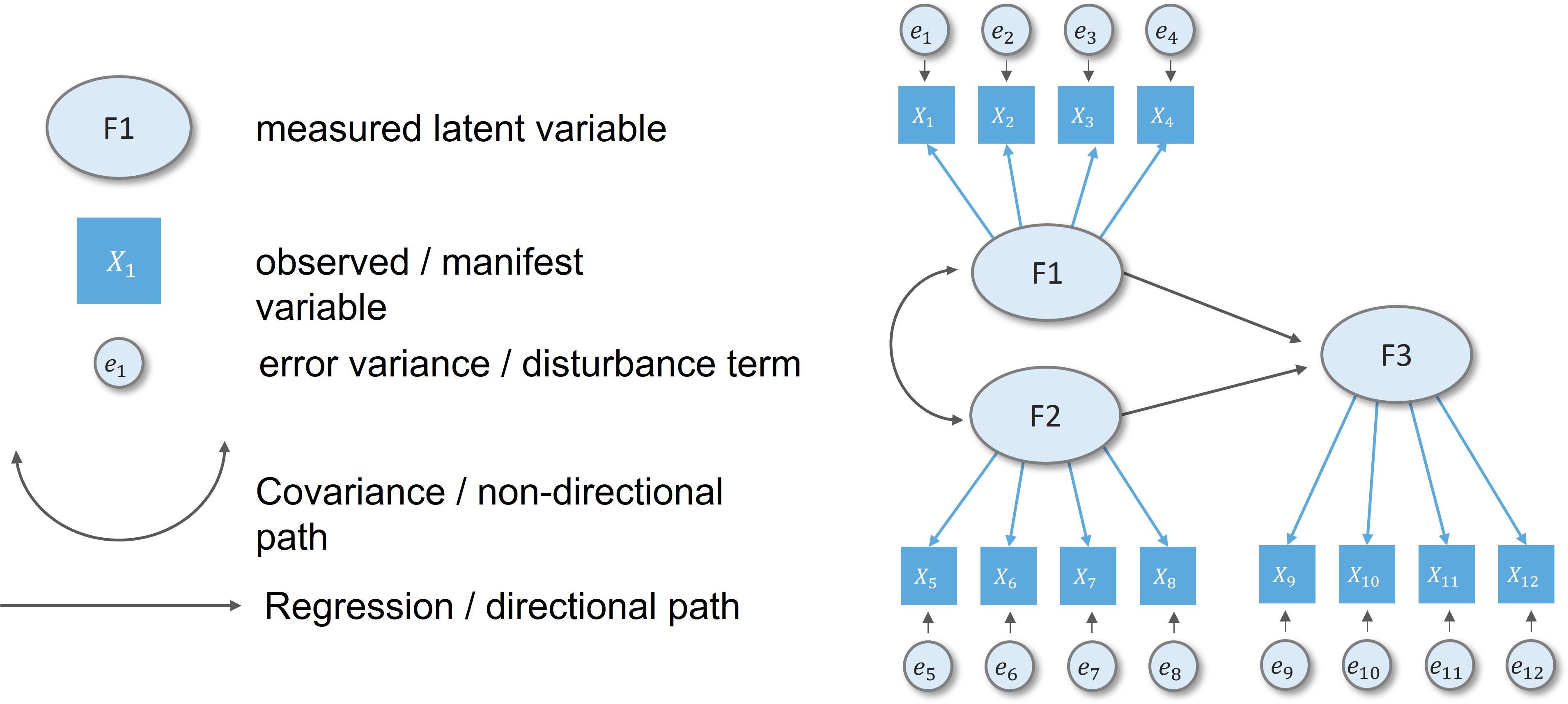
Basic SEM conventions
2. CFA-SEM with Lavaan R package
What is Lavaan?
“developed to provide useRs, researchers, and teachers a free open-source, but commercial quality”, Yves Rosseel (2012)
Check-out this lavaan tutorial
library(lavaan)
example(cfa)
cfa> ## The famous Holzinger and Swineford (1939) example
cfa> HS.model <- ' visual =~ x1 + x2 + x3
cfa+ textual =~ x4 + x5 + x6
cfa+ speed =~ x7 + x8 + x9 '
cfa> fit <- cfa(HS.model, data = HolzingerSwineford1939)
cfa> summary(fit, fit.measures = TRUE)
lavaan 0.6.13 ended normally after 35 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 21
Number of observations 301
Model Test User Model:
Test statistic 85.306
Degrees of freedom 24
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 918.852
Degrees of freedom 36
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.931
Tucker-Lewis Index (TLI) 0.896
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3737.745
Loglikelihood unrestricted model (H1) -3695.092
Akaike (AIC) 7517.490
Bayesian (BIC) 7595.339
Sample-size adjusted Bayesian (SABIC) 7528.739
Root Mean Square Error of Approximation:
RMSEA 0.092
90 Percent confidence interval - lower 0.071
90 Percent confidence interval - upper 0.114
P-value H_0: RMSEA <= 0.050 0.001
P-value H_0: RMSEA >= 0.080 0.840
Standardized Root Mean Square Residual:
SRMR 0.065
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
visual =~
x1 1.000
x2 0.554 0.100 5.554 0.000
x3 0.729 0.109 6.685 0.000
textual =~
x4 1.000
x5 1.113 0.065 17.014 0.000
x6 0.926 0.055 16.703 0.000
speed =~
x7 1.000
x8 1.180 0.165 7.152 0.000
x9 1.082 0.151 7.155 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
visual ~~
textual 0.408 0.074 5.552 0.000
speed 0.262 0.056 4.660 0.000
textual ~~
speed 0.173 0.049 3.518 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.x1 0.549 0.114 4.833 0.000
.x2 1.134 0.102 11.146 0.000
.x3 0.844 0.091 9.317 0.000
.x4 0.371 0.048 7.779 0.000
.x5 0.446 0.058 7.642 0.000
.x6 0.356 0.043 8.277 0.000
.x7 0.799 0.081 9.823 0.000
.x8 0.488 0.074 6.573 0.000
.x9 0.566 0.071 8.003 0.000
visual 0.809 0.145 5.564 0.000
textual 0.979 0.112 8.737 0.000
speed 0.384 0.086 4.451 0.000Major operators of lavaan syntax
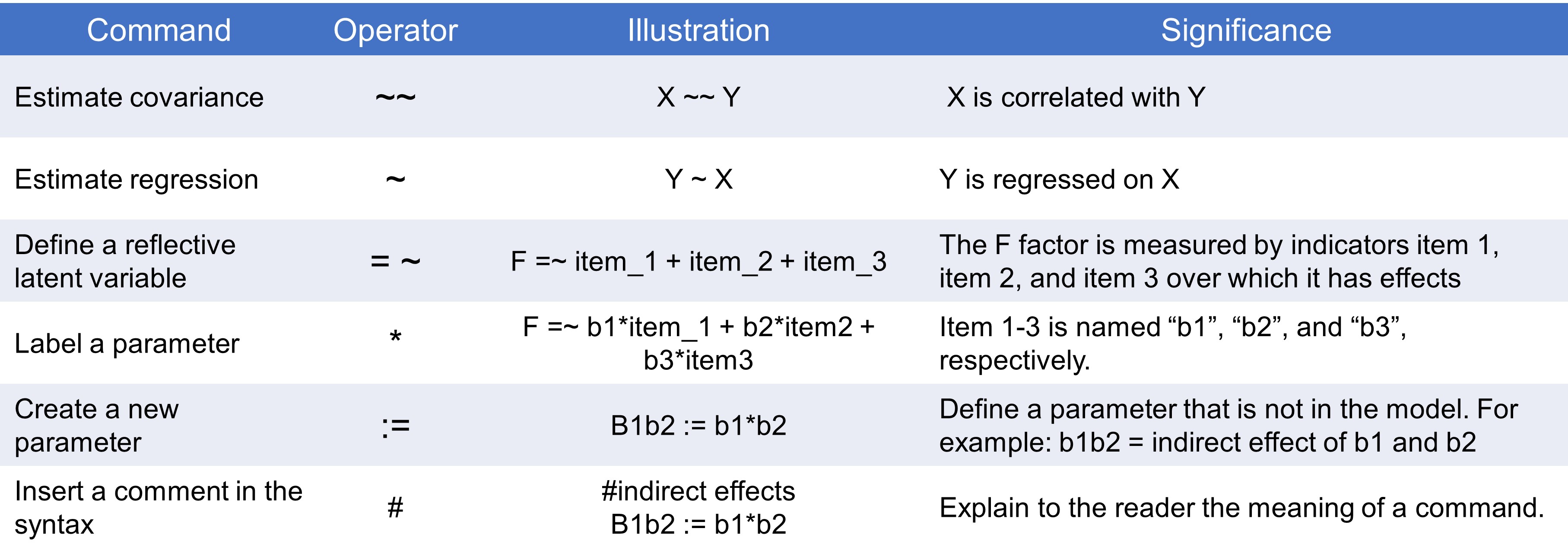
Major operators of lavaan syntax
Major operators of lavaan syntax
Major operators of lavaan syntax
Major operators of lavaan syntax
Major operators of lavaan syntax
Main steps in SEM
Defining constructs
Developing the overall measurement model
Assessing measurement model validity
Specifying the structural model
Assessing structural model validity
1. Defining Constructs
Dataset
HBAT company
HBAT is interested in understanding what affects employee’s attitudes and behaviors that contributes to employee’s retension.
Defining individual constructs
Based on literature and preliminary interviews, a study was designed focusing on five key constructs.
Job satisfaction (JS) : reactions resulting from an appraisal of one’s job situation.
Organizational commitment (OC): extent to which an employees indentifies and feels part of HBAT.
Staying intention (SI): extent to which an employee intends to continue working for HBAT.
Environmental perceptions (EP): beliefs an employee has about day-to-day, physical working conditions.
Attitudes towards cowrokers (AC): attitudes an employee has toward the coworkers he/she interacts with on a regular basis.
Defining individual constructs


Step 2. Developing overall measurement model
Developing overall measurement model
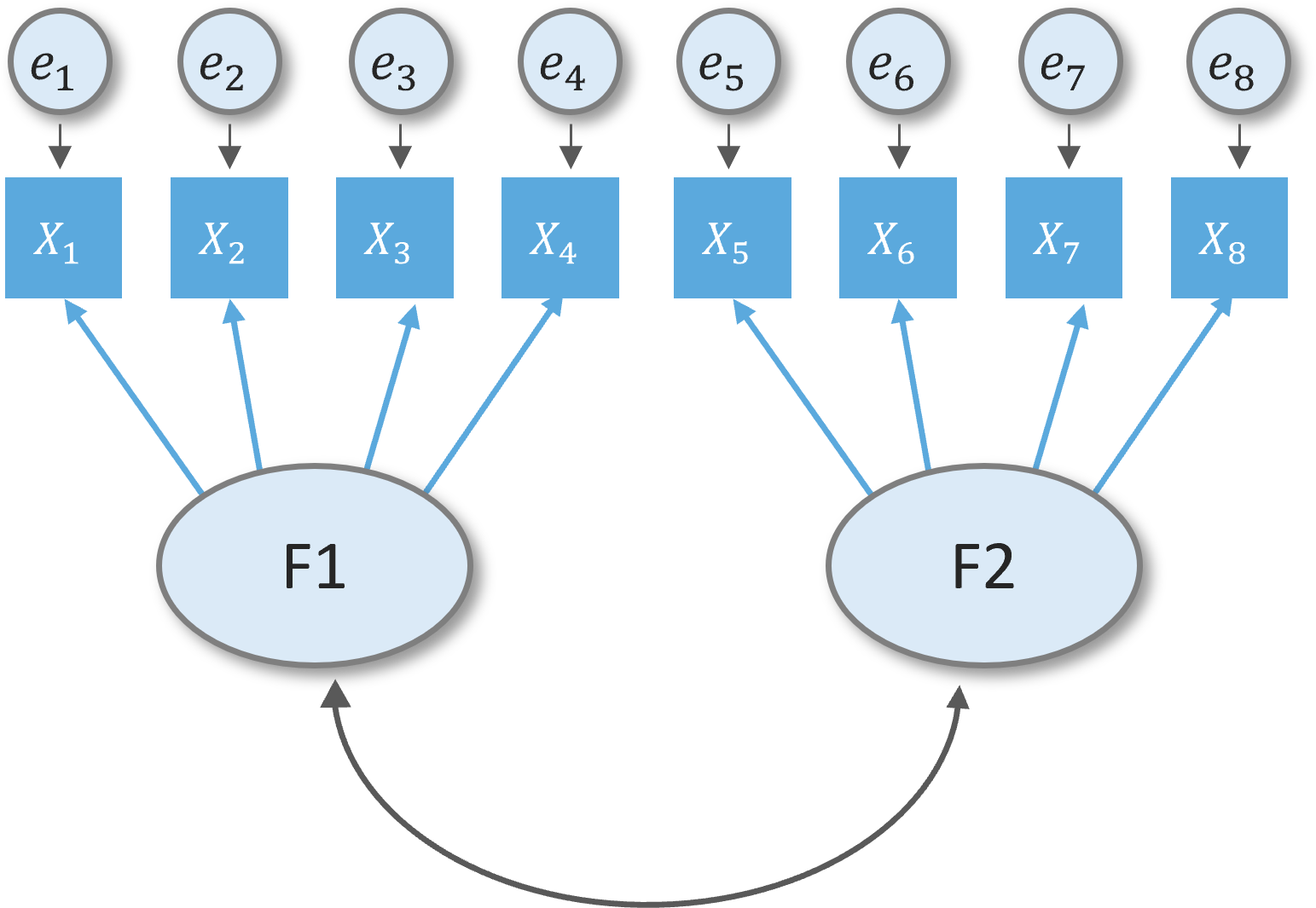
Measurement theory model (CFA) for HBAT employees
Direction of the relationship between factors is not yet defined.
Focus on confirming the specified model with empirical model (using empirical data), hence confirmatory.
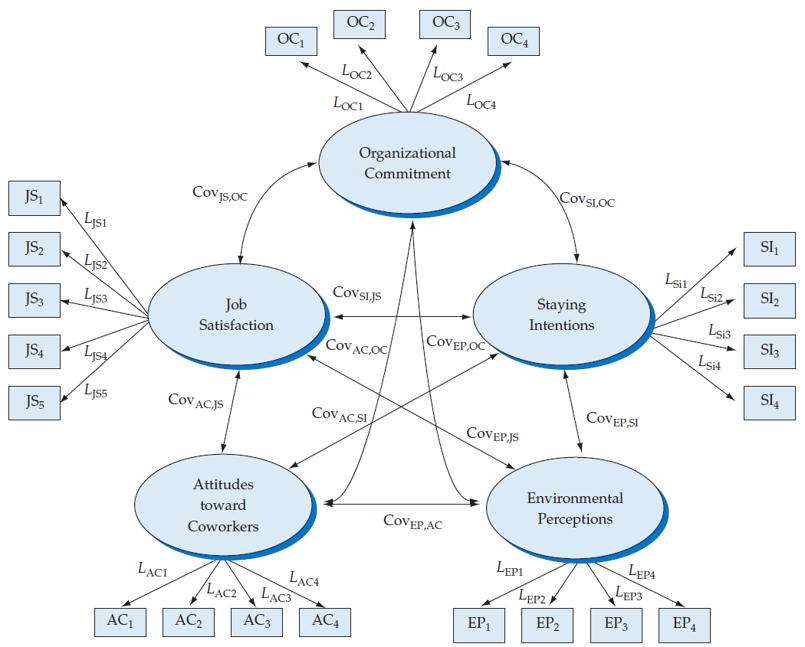
Let’s practice!
Step 3. Assessing measurement model validity
Basic principles
Compare covariance matrix of the research data \(\text{S}\) and reproduced covariance \(\Sigma\)
Hypothesis:
Null: \(\text{S} = \Sigma\)
Atternative: \(\text{S} \ne \Sigma\)
Idea is to arrived with a parameter that minimizes the difference of \(\text{S}\) and \(\Sigma\)
cfa_fit <- cfa(cfa_model, data = hbat_data)
cfa_fit %>% summary()
lavaan 0.6.13 ended normally after 54 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 52
Number of observations 400
Model Test User Model:
Test statistic 240.738
Degrees of freedom 179
P-value (Chi-square) 0.001
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
SI =~
SI1 1.000
SI2 1.073 0.055 19.563 0.000
SI3 1.065 0.066 16.053 0.000
SI4 1.167 0.061 19.230 0.000
JS =~
JS1 1.000
JS2 1.033 0.075 13.683 0.000
JS3 0.902 0.072 12.516 0.000
JS4 0.910 0.070 12.958 0.000
JS5 15.190 1.132 13.414 0.000
AC =~
AC1 1.000
AC2 1.236 0.067 18.392 0.000
AC3 1.037 0.055 18.870 0.000
AC4 1.146 0.063 18.255 0.000
EP =~
EP1 1.000
EP2 1.033 0.073 14.083 0.000
EP3 0.821 0.060 13.734 0.000
EP4 0.914 0.064 14.335 0.000
OC =~
OC1 1.000
OC2 1.314 0.108 12.209 0.000
OC3 0.783 0.076 10.322 0.000
OC4 1.165 0.097 11.968 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
SI ~~
JS 0.161 0.042 3.834 0.000
AC 0.249 0.048 5.161 0.000
EP 0.502 0.065 7.733 0.000
OC 0.574 0.080 7.191 0.000
JS ~~
AC 0.057 0.065 0.868 0.386
EP 0.303 0.078 3.892 0.000
OC 0.304 0.090 3.390 0.001
AC ~~
EP 0.372 0.088 4.251 0.000
OC 0.517 0.107 4.842 0.000
EP ~~
OC 0.925 0.143 6.469 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.SI1 0.258 0.023 11.121 0.000
.SI2 0.195 0.021 9.479 0.000
.SI3 0.464 0.038 12.264 0.000
.SI4 0.256 0.026 9.952 0.000
.JS1 0.807 0.074 10.960 0.000
.JS2 0.825 0.076 10.822 0.000
.JS3 0.930 0.078 11.910 0.000
.JS4 0.824 0.071 11.570 0.000
.JS5 196.867 17.681 11.135 0.000
.AC1 0.628 0.059 10.566 0.000
.AC2 0.973 0.092 10.617 0.000
.AC3 0.601 0.059 10.114 0.000
.AC4 0.867 0.081 10.742 0.000
.EP1 1.744 0.143 12.222 0.000
.EP2 0.937 0.091 10.245 0.000
.EP3 0.699 0.064 10.860 0.000
.EP4 0.637 0.066 9.659 0.000
.OC1 4.196 0.318 13.177 0.000
.OC2 1.029 0.149 6.929 0.000
.OC3 1.745 0.137 12.700 0.000
.OC4 1.267 0.138 9.193 0.000
SI 0.498 0.052 9.526 0.000
JS 0.981 0.122 8.038 0.000
AC 1.309 0.135 9.664 0.000
EP 1.600 0.214 7.471 0.000
OC 2.164 0.357 6.058 0.000Basic principles
Compare covariance matrix of the research data \(\text{S}\) and reproduced covariance \(\Sigma\)
Hypothesis:
Null: \(\text{S} = \Sigma\)
Atternative: \(\text{S} \ne \Sigma\)
Idea is to arrived with a parameter that minimizes the difference of \(\text{S}\) and \(\Sigma\)

Basic principles
To understand the SEM process, consider the Table on the right.
e.g., iterative procedure using least square method.
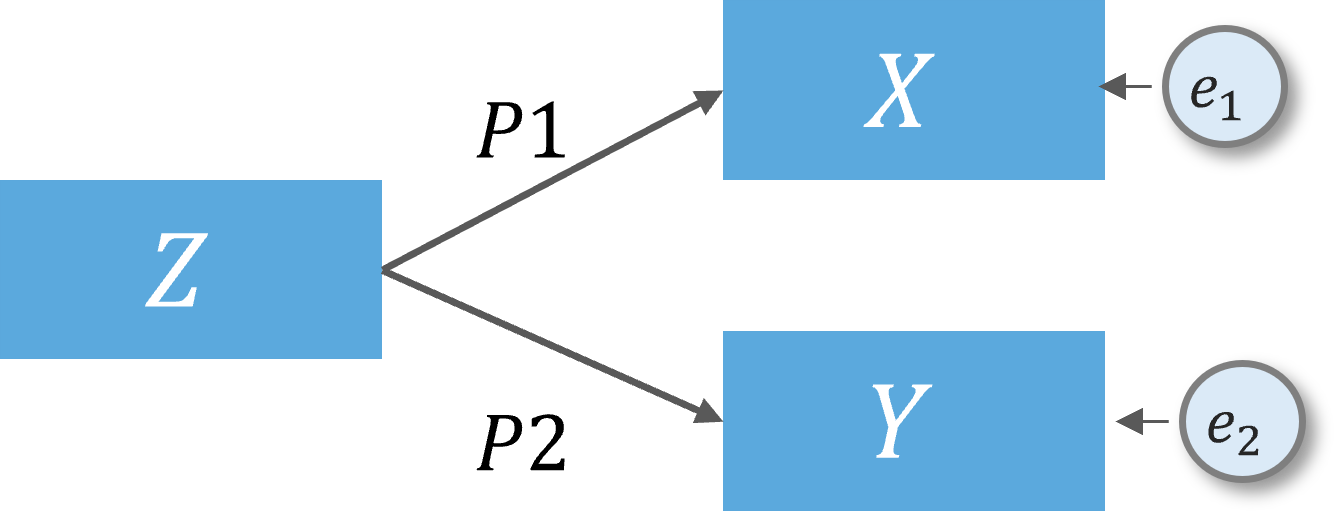

Summary output
Overall results
Loadings
Variances
cfa_fit <- cfa(cfa_model, data = hbat_data)
summary(cfa_fit)
lavaan 0.6.13 ended normally after 54 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 52
Number of observations 400
Model Test User Model:
Test statistic 240.738
Degrees of freedom 179
P-value (Chi-square) 0.001
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
SI =~
SI1 1.000
SI2 1.073 0.055 19.563 0.000
SI3 1.065 0.066 16.053 0.000
SI4 1.167 0.061 19.230 0.000
JS =~
JS1 1.000
JS2 1.033 0.075 13.683 0.000
JS3 0.902 0.072 12.516 0.000
JS4 0.910 0.070 12.958 0.000
JS5 15.190 1.132 13.414 0.000
AC =~
AC1 1.000
AC2 1.236 0.067 18.392 0.000
AC3 1.037 0.055 18.870 0.000
AC4 1.146 0.063 18.255 0.000
EP =~
EP1 1.000
EP2 1.033 0.073 14.083 0.000
EP3 0.821 0.060 13.734 0.000
EP4 0.914 0.064 14.335 0.000
OC =~
OC1 1.000
OC2 1.314 0.108 12.209 0.000
OC3 0.783 0.076 10.322 0.000
OC4 1.165 0.097 11.968 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
SI ~~
JS 0.161 0.042 3.834 0.000
AC 0.249 0.048 5.161 0.000
EP 0.502 0.065 7.733 0.000
OC 0.574 0.080 7.191 0.000
JS ~~
AC 0.057 0.065 0.868 0.386
EP 0.303 0.078 3.892 0.000
OC 0.304 0.090 3.390 0.001
AC ~~
EP 0.372 0.088 4.251 0.000
OC 0.517 0.107 4.842 0.000
EP ~~
OC 0.925 0.143 6.469 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.SI1 0.258 0.023 11.121 0.000
.SI2 0.195 0.021 9.479 0.000
.SI3 0.464 0.038 12.264 0.000
.SI4 0.256 0.026 9.952 0.000
.JS1 0.807 0.074 10.960 0.000
.JS2 0.825 0.076 10.822 0.000
.JS3 0.930 0.078 11.910 0.000
.JS4 0.824 0.071 11.570 0.000
.JS5 196.867 17.681 11.135 0.000
.AC1 0.628 0.059 10.566 0.000
.AC2 0.973 0.092 10.617 0.000
.AC3 0.601 0.059 10.114 0.000
.AC4 0.867 0.081 10.742 0.000
.EP1 1.744 0.143 12.222 0.000
.EP2 0.937 0.091 10.245 0.000
.EP3 0.699 0.064 10.860 0.000
.EP4 0.637 0.066 9.659 0.000
.OC1 4.196 0.318 13.177 0.000
.OC2 1.029 0.149 6.929 0.000
.OC3 1.745 0.137 12.700 0.000
.OC4 1.267 0.138 9.193 0.000
SI 0.498 0.052 9.526 0.000
JS 0.981 0.122 8.038 0.000
AC 1.309 0.135 9.664 0.000
EP 1.600 0.214 7.471 0.000
OC 2.164 0.357 6.058 0.000Summary output
Overall results
Degrees of freedom (df)
- \(df = \frac{1}{2} p (p + 1) - k\)
- \(p\) = total observed variables
- \(k\) = total estimated parameters
Identification
- Include at least three manifest variables
- Create models with \(df > 0\)
cfa_fit <- cfa(cfa_model, data = hbat_data)
summary(cfa_fit)
lavaan 0.6.13 ended normally after 54 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 52
Number of observations 400
Model Test User Model:
Test statistic 240.738
Degrees of freedom 179
P-value (Chi-square) 0.001
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
SI =~
SI1 1.000
SI2 1.073 0.055 19.563 0.000
SI3 1.065 0.066 16.053 0.000
SI4 1.167 0.061 19.230 0.000
JS =~
JS1 1.000
JS2 1.033 0.075 13.683 0.000
JS3 0.902 0.072 12.516 0.000
JS4 0.910 0.070 12.958 0.000
JS5 15.190 1.132 13.414 0.000
AC =~
AC1 1.000
AC2 1.236 0.067 18.392 0.000
AC3 1.037 0.055 18.870 0.000
AC4 1.146 0.063 18.255 0.000
EP =~
EP1 1.000
EP2 1.033 0.073 14.083 0.000
EP3 0.821 0.060 13.734 0.000
EP4 0.914 0.064 14.335 0.000
OC =~
OC1 1.000
OC2 1.314 0.108 12.209 0.000
OC3 0.783 0.076 10.322 0.000
OC4 1.165 0.097 11.968 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
SI ~~
JS 0.161 0.042 3.834 0.000
AC 0.249 0.048 5.161 0.000
EP 0.502 0.065 7.733 0.000
OC 0.574 0.080 7.191 0.000
JS ~~
AC 0.057 0.065 0.868 0.386
EP 0.303 0.078 3.892 0.000
OC 0.304 0.090 3.390 0.001
AC ~~
EP 0.372 0.088 4.251 0.000
OC 0.517 0.107 4.842 0.000
EP ~~
OC 0.925 0.143 6.469 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.SI1 0.258 0.023 11.121 0.000
.SI2 0.195 0.021 9.479 0.000
.SI3 0.464 0.038 12.264 0.000
.SI4 0.256 0.026 9.952 0.000
.JS1 0.807 0.074 10.960 0.000
.JS2 0.825 0.076 10.822 0.000
.JS3 0.930 0.078 11.910 0.000
.JS4 0.824 0.071 11.570 0.000
.JS5 196.867 17.681 11.135 0.000
.AC1 0.628 0.059 10.566 0.000
.AC2 0.973 0.092 10.617 0.000
.AC3 0.601 0.059 10.114 0.000
.AC4 0.867 0.081 10.742 0.000
.EP1 1.744 0.143 12.222 0.000
.EP2 0.937 0.091 10.245 0.000
.EP3 0.699 0.064 10.860 0.000
.EP4 0.637 0.066 9.659 0.000
.OC1 4.196 0.318 13.177 0.000
.OC2 1.029 0.149 6.929 0.000
.OC3 1.745 0.137 12.700 0.000
.OC4 1.267 0.138 9.193 0.000
SI 0.498 0.052 9.526 0.000
JS 0.981 0.122 8.038 0.000
AC 1.309 0.135 9.664 0.000
EP 1.600 0.214 7.471 0.000
OC 2.164 0.357 6.058 0.000Summary output
Loadings
- Measures the strength of the relationship between items and factor.
cfa_fit <- cfa(cfa_model, data = hbat_data)
summary(cfa_fit, standardized = TRUE)
lavaan 0.6.13 ended normally after 54 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 52
Number of observations 400
Model Test User Model:
Test statistic 240.738
Degrees of freedom 179
P-value (Chi-square) 0.001
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
SI =~
SI1 1.000 0.706 0.811
SI2 1.073 0.055 19.563 0.000 0.757 0.864
SI3 1.065 0.066 16.053 0.000 0.752 0.741
SI4 1.167 0.061 19.230 0.000 0.823 0.852
JS =~
JS1 1.000 0.991 0.741
JS2 1.033 0.075 13.683 0.000 1.023 0.748
JS3 0.902 0.072 12.516 0.000 0.894 0.680
JS4 0.910 0.070 12.958 0.000 0.902 0.705
JS5 15.190 1.132 13.414 0.000 15.046 0.731
AC =~
AC1 1.000 1.144 0.822
AC2 1.236 0.067 18.392 0.000 1.414 0.820
AC3 1.037 0.055 18.870 0.000 1.187 0.837
AC4 1.146 0.063 18.255 0.000 1.312 0.815
EP =~
EP1 1.000 1.265 0.692
EP2 1.033 0.073 14.083 0.000 1.307 0.803
EP3 0.821 0.060 13.734 0.000 1.038 0.779
EP4 0.914 0.064 14.335 0.000 1.156 0.823
OC =~
OC1 1.000 1.471 0.583
OC2 1.314 0.108 12.209 0.000 1.934 0.886
OC3 0.783 0.076 10.322 0.000 1.151 0.657
OC4 1.165 0.097 11.968 0.000 1.714 0.836
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
SI ~~
JS 0.161 0.042 3.834 0.000 0.230 0.230
AC 0.249 0.048 5.161 0.000 0.309 0.309
EP 0.502 0.065 7.733 0.000 0.562 0.562
OC 0.574 0.080 7.191 0.000 0.553 0.553
JS ~~
AC 0.057 0.065 0.868 0.386 0.050 0.050
EP 0.303 0.078 3.892 0.000 0.242 0.242
OC 0.304 0.090 3.390 0.001 0.209 0.209
AC ~~
EP 0.372 0.088 4.251 0.000 0.257 0.257
OC 0.517 0.107 4.842 0.000 0.307 0.307
EP ~~
OC 0.925 0.143 6.469 0.000 0.497 0.497
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.SI1 0.258 0.023 11.121 0.000 0.258 0.342
.SI2 0.195 0.021 9.479 0.000 0.195 0.253
.SI3 0.464 0.038 12.264 0.000 0.464 0.451
.SI4 0.256 0.026 9.952 0.000 0.256 0.274
.JS1 0.807 0.074 10.960 0.000 0.807 0.451
.JS2 0.825 0.076 10.822 0.000 0.825 0.441
.JS3 0.930 0.078 11.910 0.000 0.930 0.538
.JS4 0.824 0.071 11.570 0.000 0.824 0.503
.JS5 196.867 17.681 11.135 0.000 196.867 0.465
.AC1 0.628 0.059 10.566 0.000 0.628 0.324
.AC2 0.973 0.092 10.617 0.000 0.973 0.327
.AC3 0.601 0.059 10.114 0.000 0.601 0.299
.AC4 0.867 0.081 10.742 0.000 0.867 0.335
.EP1 1.744 0.143 12.222 0.000 1.744 0.522
.EP2 0.937 0.091 10.245 0.000 0.937 0.354
.EP3 0.699 0.064 10.860 0.000 0.699 0.393
.EP4 0.637 0.066 9.659 0.000 0.637 0.323
.OC1 4.196 0.318 13.177 0.000 4.196 0.660
.OC2 1.029 0.149 6.929 0.000 1.029 0.216
.OC3 1.745 0.137 12.700 0.000 1.745 0.568
.OC4 1.267 0.138 9.193 0.000 1.267 0.301
SI 0.498 0.052 9.526 0.000 1.000 1.000
JS 0.981 0.122 8.038 0.000 1.000 1.000
AC 1.309 0.135 9.664 0.000 1.000 1.000
EP 1.600 0.214 7.471 0.000 1.000 1.000
OC 2.164 0.357 6.058 0.000 1.000 1.000Summary output
Variances
Refer to unique variance that the factor unable to account for. Similar to error term in OLS, hence it is also term as error variance.
cfa_fit <- cfa(cfa_model, data = hbat_data)
summary(cfa_fit, standardized = TRUE)
lavaan 0.6.13 ended normally after 54 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 52
Number of observations 400
Model Test User Model:
Test statistic 240.738
Degrees of freedom 179
P-value (Chi-square) 0.001
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
SI =~
SI1 1.000 0.706 0.811
SI2 1.073 0.055 19.563 0.000 0.757 0.864
SI3 1.065 0.066 16.053 0.000 0.752 0.741
SI4 1.167 0.061 19.230 0.000 0.823 0.852
JS =~
JS1 1.000 0.991 0.741
JS2 1.033 0.075 13.683 0.000 1.023 0.748
JS3 0.902 0.072 12.516 0.000 0.894 0.680
JS4 0.910 0.070 12.958 0.000 0.902 0.705
JS5 15.190 1.132 13.414 0.000 15.046 0.731
AC =~
AC1 1.000 1.144 0.822
AC2 1.236 0.067 18.392 0.000 1.414 0.820
AC3 1.037 0.055 18.870 0.000 1.187 0.837
AC4 1.146 0.063 18.255 0.000 1.312 0.815
EP =~
EP1 1.000 1.265 0.692
EP2 1.033 0.073 14.083 0.000 1.307 0.803
EP3 0.821 0.060 13.734 0.000 1.038 0.779
EP4 0.914 0.064 14.335 0.000 1.156 0.823
OC =~
OC1 1.000 1.471 0.583
OC2 1.314 0.108 12.209 0.000 1.934 0.886
OC3 0.783 0.076 10.322 0.000 1.151 0.657
OC4 1.165 0.097 11.968 0.000 1.714 0.836
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
SI ~~
JS 0.161 0.042 3.834 0.000 0.230 0.230
AC 0.249 0.048 5.161 0.000 0.309 0.309
EP 0.502 0.065 7.733 0.000 0.562 0.562
OC 0.574 0.080 7.191 0.000 0.553 0.553
JS ~~
AC 0.057 0.065 0.868 0.386 0.050 0.050
EP 0.303 0.078 3.892 0.000 0.242 0.242
OC 0.304 0.090 3.390 0.001 0.209 0.209
AC ~~
EP 0.372 0.088 4.251 0.000 0.257 0.257
OC 0.517 0.107 4.842 0.000 0.307 0.307
EP ~~
OC 0.925 0.143 6.469 0.000 0.497 0.497
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.SI1 0.258 0.023 11.121 0.000 0.258 0.342
.SI2 0.195 0.021 9.479 0.000 0.195 0.253
.SI3 0.464 0.038 12.264 0.000 0.464 0.451
.SI4 0.256 0.026 9.952 0.000 0.256 0.274
.JS1 0.807 0.074 10.960 0.000 0.807 0.451
.JS2 0.825 0.076 10.822 0.000 0.825 0.441
.JS3 0.930 0.078 11.910 0.000 0.930 0.538
.JS4 0.824 0.071 11.570 0.000 0.824 0.503
.JS5 196.867 17.681 11.135 0.000 196.867 0.465
.AC1 0.628 0.059 10.566 0.000 0.628 0.324
.AC2 0.973 0.092 10.617 0.000 0.973 0.327
.AC3 0.601 0.059 10.114 0.000 0.601 0.299
.AC4 0.867 0.081 10.742 0.000 0.867 0.335
.EP1 1.744 0.143 12.222 0.000 1.744 0.522
.EP2 0.937 0.091 10.245 0.000 0.937 0.354
.EP3 0.699 0.064 10.860 0.000 0.699 0.393
.EP4 0.637 0.066 9.659 0.000 0.637 0.323
.OC1 4.196 0.318 13.177 0.000 4.196 0.660
.OC2 1.029 0.149 6.929 0.000 1.029 0.216
.OC3 1.745 0.137 12.700 0.000 1.745 0.568
.OC4 1.267 0.138 9.193 0.000 1.267 0.301
SI 0.498 0.052 9.526 0.000 1.000 1.000
JS 0.981 0.122 8.038 0.000 1.000 1.000
AC 1.309 0.135 9.664 0.000 1.000 1.000
EP 1.600 0.214 7.471 0.000 1.000 1.000
OC 2.164 0.357 6.058 0.000 1.000 1.000Fit indices
Goodness of fit indices
- Goodness-of-fit index (GFI)
- Adjusted goodness-fit-index (AGFI)
- Comparative fit index (CFI)
- Normed fit index (NFI)
- Non-normed fit index (NNF)
Badness of fit indices
- Standard root mean square of the residuals (SRMR)
- Root mean square error of approximation (RMSEA)
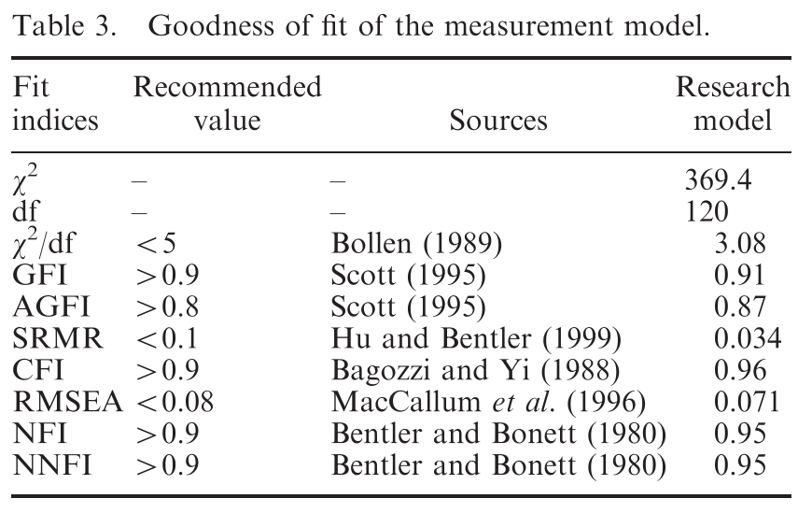
Fit indices
Goodness of fit indices
Goodness-of-fit index (GFI)
Adjusted goodness-fit-index (AGFI)
Comparative fit index (CFI)
Normed fit index (NFI)
Non-normed fit index (NNF)
fitMeasures(cfa_fit)
npar fmin chisq
52.000 0.301 240.738
df pvalue baseline.chisq
179.000 0.001 4452.567
baseline.df baseline.pvalue cfi
210.000 0.000 0.985
tli nnfi rfi
0.983 0.983 0.937
nfi pnfi ifi
0.946 0.806 0.986
rni logl unrestricted.logl
0.985 -13916.782 -13796.413
aic bic ntotal
27937.564 28145.120 400.000
bic2 rmsea rmsea.ci.lower
27980.120 0.029 0.019
rmsea.ci.upper rmsea.ci.level rmsea.pvalue
0.039 0.900 1.000
rmsea.close.h0 rmsea.notclose.pvalue rmsea.notclose.h0
0.050 0.000 0.080
rmr rmr_nomean srmr
0.414 0.414 0.036
srmr_bentler srmr_bentler_nomean crmr
0.036 0.036 0.037
crmr_nomean srmr_mplus srmr_mplus_nomean
0.037 0.036 0.036
cn_05 cn_01 gfi
351.949 376.401 0.947
agfi pgfi mfi
0.932 0.734 0.926
ecvi
0.862 Fit indices
Goodness of fit indices
Goodness-of-fit index (GFI)
Adjusted goodness-fit-index (AGFI)
Comparative fit index (CFI)
Normed fit index (NFI)
Non-normed fit index (NNF)
Fit indices
Reliability and validity test
Reliability test
- Composite reliability
Validity test
Convergent validity
Discriminant validity
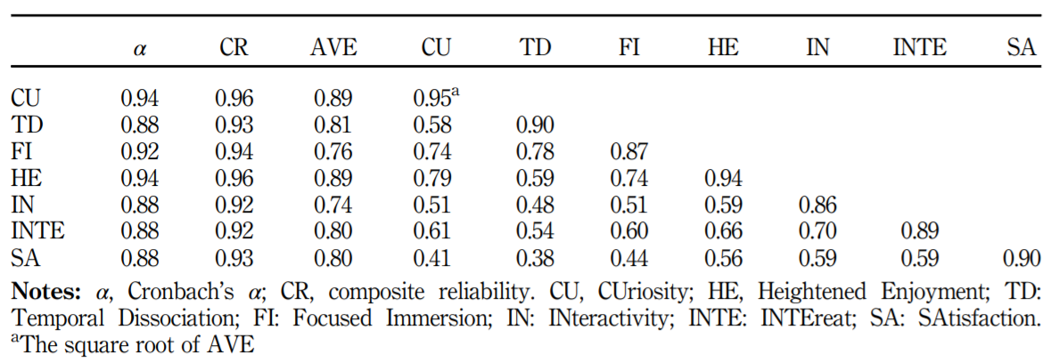
Reliability and validity test
Composite reliability:
alpha>0.70Convergent validity: AVE (
avevar) >0.50Discriminant validity:
omega>0.7
Let’s practice
Step 4: Specifying the structural model
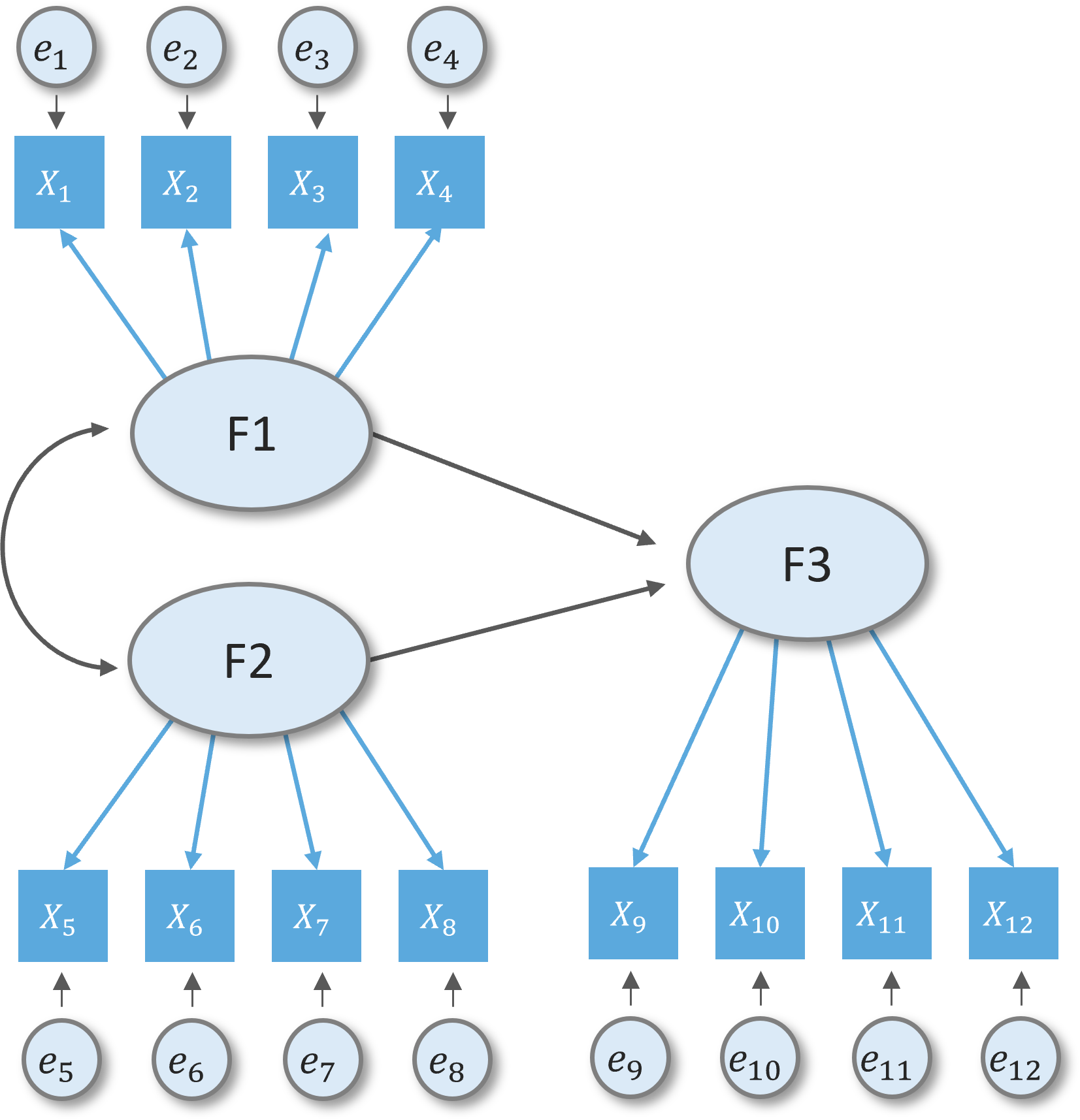
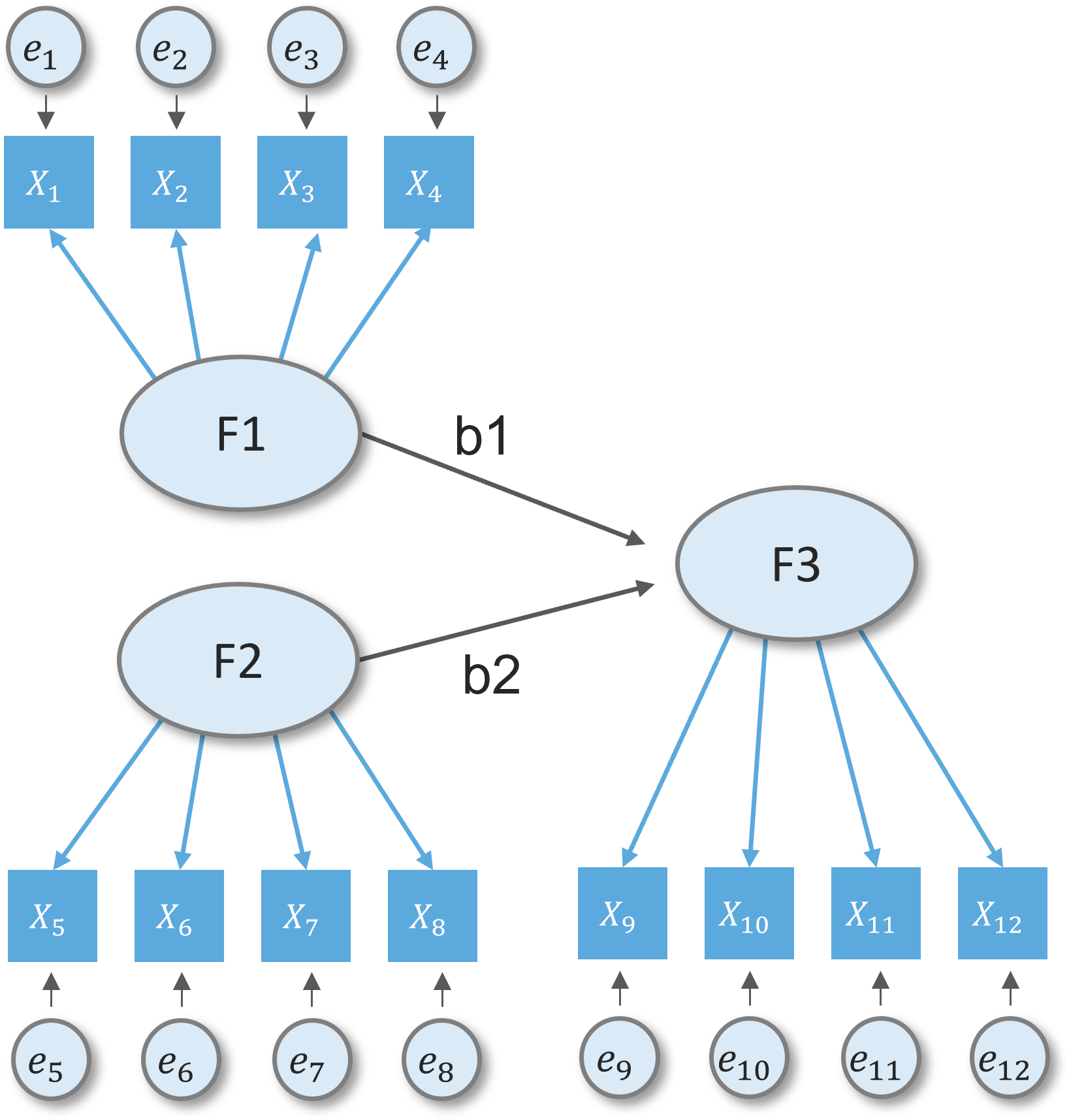
CFA model to structural model

Defining structural model
Hypotheses:
H1: Environmental perceptions are positively related to job satisfaction.
H2: Environmental perceptions are positively related to organizational commitment.
H3: Attitudes toward coworkers are positively related to job satisfaction.
H4: Attitudes toward coworkers are positively related to organizational commitment.
H5: Job satisfaction is related positively to organizational commitment.
H6: Job satisfaction is related positively to staying intentions.
H7: Organizational commitment is related positively to staying intention.
Defining structural model
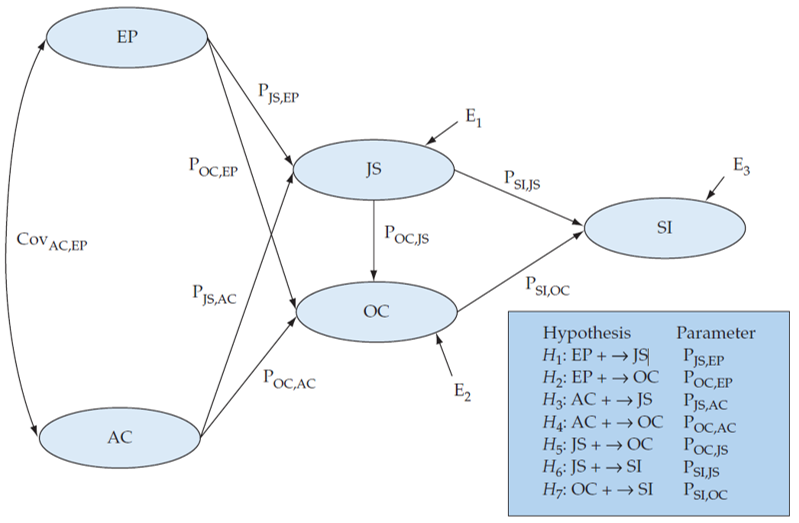
Let’s practice
Defining structural model
Defining structural model
GOF measures between structural and CFA model
gof_indices <- c('chisq', 'df','pvalue', "gfi",
'rmsea', 'rmr', 'srmr', 'nfi',
'nnfi', 'cfi', 'agfi')
fitmeasures(sem_fit, fit.measures = gof_indices)
chisq df pvalue gfi rmsea rmr srmr nfi nnfi cfi
287.179 181.000 0.000 0.938 0.038 0.410 0.060 0.936 0.971 0.975
agfi
0.921
fitmeasures(cfa_fit, fit.measures = gof_indices)
chisq df pvalue gfi rmsea rmr srmr nfi nnfi cfi
240.738 179.000 0.001 0.947 0.029 0.414 0.036 0.946 0.983 0.985
agfi
0.932 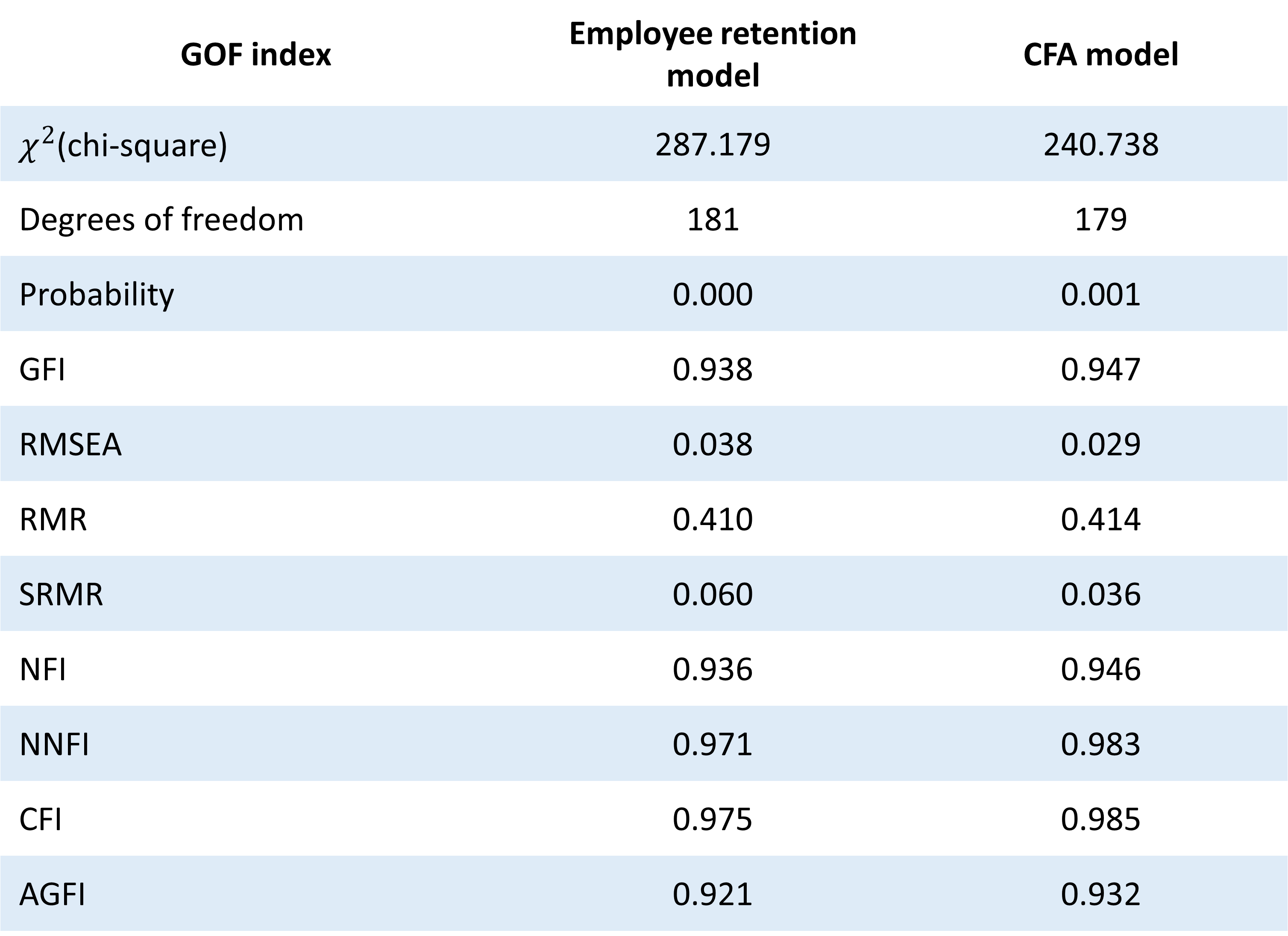
What’s next?
Modification indeces
Handling heywood cases
Comparing competing models
Formative scales in SEM
Higher-order factor analysis
Multigroup analysis

Thank you!

CFA & CB SEM